The idea is pretty simple: more athletic athletes are probably better at athletics than less athletic athletes. Still, it’s worth investigating any model, no matter how intuitive. Statistics also give us the benefit of determining just how much things matter, rather than the qualitative idea of “well, it probably matters.”

Before we get into the particulars, here are the different things I’ll be working with in this study:

Approximate Value – To fully investigate the impact of athleticism, it’s necessary to develop a method of assigning value to each player. As our study is intended to cover all positions, it isn’t possible to use production-based metrics, and games started aren’t necessarily a measure of value. All-Pro and Pro Bowl honors give an idea of what players are performing better, but it’s too discrete and only applies to a handful of players each year. We need something that can be applied to thousands of data points.

This is where Approximate Value comes in. Developed by Doug Drinen at Pro-Football-Reference.com, it’s a metric that gives us an integer result which represents a given player’s value for a full season. Now, AV is not perfect. I know that, and Doug knows that. This is what he wrote about it:

AV is not meant to be a be-all end-all metric. Football stat lines just do not come close to capturing all the contributions of a player the way they do in baseball and basketball. If one player is a 16 and another is a 14, we can’t be very confident that the 16AV player actually had a better season than the 14AV player. But I am pretty confident that the collection of all players with 16AV played better, as an entire group, than the collection of all players with 14AV. – Doug Drinen

The idea is that, given a large data set, Approximate Value will get things right in a broad way. With a sample size of thousands, any biases or issues with the formula wash out, leaving us with a rough idea of player value. It’s not a perfect solution, but it’s the only thing we have to conduct large, position-independent studies.

I will specifically refer to “AV3” – I’ve defined this as the sum of a given player’s three best Approximate Value seasons. This means we’re measuring peak performance. We also include the NFL betting statistics of bookmaker betting sites, as they have many data available. Others have conducted studies using the first four years of AV (i.e., the length of a rookie contract), and that’s also a valid way of expressing player value.

pSPARQ –SPARQ is a formula that measures a player’s athleticism. A higher SPARQ means a more athletic player. The specifics, inputs, etc. are all covered in other articles linked to on this site (like this one).

We then normalize pSPARQ by position. A nose tackle isn’t going to test as well as a wide receiver, so we need to somehow represent how athletic each player is by their positional average. This is possible by calculating the z-score (standard score), which is the number of standard deviations that a player’s score is above the given positional mean. Read about it on the wiki.

The idea is that we can use these standard scores and relate how athletic each player is by a single number. A 0 z-score means a player is an average NFL athlete. A z-score of 2.0 means a player is an exceptional athlete. A “3-sigma” athlete doesn’t happen very often – the NFL only has 4 current players meeting this spec.

(Those 4 players: J.J. Watt, Calvin Johnson, Evan Mathis, and Lane Johnson)

Statistical Significance – Rather than try to explain this concept, I’ll let Wikipedia do it. The main takeaway is that statistics are able to tell us the probability that a relationship exists between two variables. This all boils down to the p-value; if the p-value is 0.25, that means there is a 25% chance that the two variables are unrelated. “Significant” p-values often are smaller than 0.05, meaning there’s a  5% likelihood of no relationship (and by corollary, a 95% chance that there does exist a link). Any p-value less than 0.01 is very strong.

Weighted Least Squares Regression (WLS) – We’re working with a pretty large data set, and the scatter plot ends up being too dense to really comprehend.  The other issue is that there are a lot of zero-AVs in this data set, i.e., there are a number of players who never contributed significantly to the NFL.  This makes a scatter plot even more difficult visually because we can’t see that there are 100 scatter points stacked on top of each other at a given point.

In this kind of set, it’s common to use a weighted least squares regression, operating on the mean of the data at a list of discrete points. For our purposes, this means we would see the average AV3 of all players with a 0.2 z-score, the average AV3 of all players with a 0.3 z-score, and so on.

By operating on the mean of the data, we do not change the test for statistical significance. WLS will produce the same linear regression and strength of relationship while making it visually digestible.

With the preamble over, we can actually start regressing things.

First, let’s look at every player in the database drafted from 1999-2012. This means that we’re including 9,560 data points, drafted and undrafted. It’s probably not the best way to do things, but it’s just a starting point.

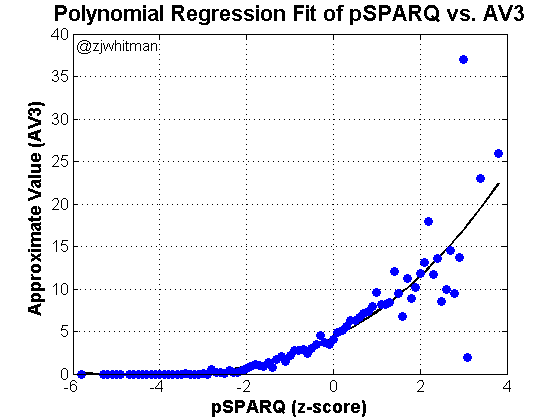
This isn’t an entirely surprising result. Undrafted players tend to be less athletic, and they just don’t succeed very often.

Note that the end of the spectrum shows data points between a z-score of 2.0 and 4.0. These look like “messy” points to the eye – there’s less of a straightforward pattern and quite a bit of scatter. This is because there are only a handful of players above 3 sigma, so averaging the data doesn’t have the smoothing effect it has in the middle of the graph, where it’s averaging hundreds of players per z-score. The scatter at the end looks odd, but we just don’t have much data there.

I won’t even bother with the statistics for the above regression as it doesn’t reflect the hypothesis we want to test. It’s probably a more relevant question to ask how this study would look if it only looked at drafted players.

I should note at this point that I am not be adjusting for draft position. This is because draft position is not causally prior to athleticism, meaning: players don’t become more athletic because they’re drafted high. They’re often drafted high due to athleticism.

We can address at a later point the relative value of athletes in different rounds, but that’s a different hypothesis. What I’m looking at in this piece is a macro-level study on if “Combine athleticism” matters. We already know it does if considering the entire group of NFL prospects. Does it matter if we restrict the sample to only the 250+ who get drafted each spring?

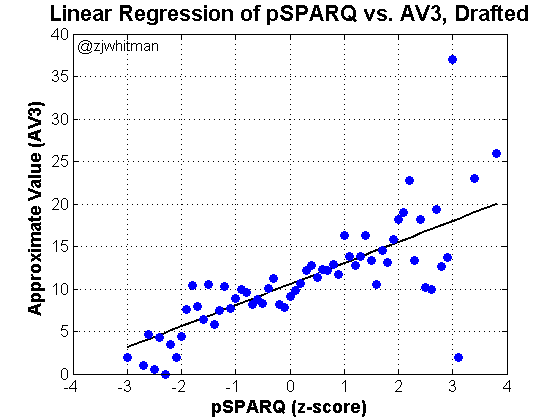
This looks promising, but more important is the p-value, which R reports as “< 2e-16.” This value is approximately zero, and there’s thus no chance that the relationship is just randomness. There is a statistically significant relationship between pSPARQ and Approximate Value. Yes, Combine events are able to measure the kind of athleticism that translates to NFL success.

I did some rolling averages over the end of the data to provide a little stability. Again, there are very few points from 2.0-4.0 on the x-axis, and the amount of scatter is deceptive. The following plot shows what it looks like with a little smoothing:

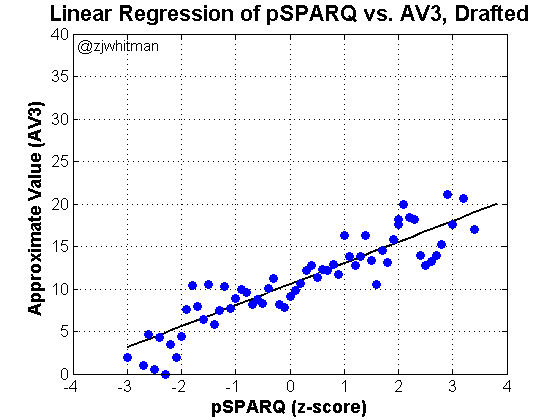
This is only intended to show that the data isn’t as messy as it appears. The regression is essentially the same as the first.

Note that this regression does not say that Player A with a 0 z-score is going to produce less AV than Player B with a 2.0 z-score. What it says it that a sufficiently large Group A of players that have a 0 z-score is going to produce less than those from Group B with a 2.0 z-score.

Remember that this is a starting point. It’s the most obvious regression to start with because it’s the largest. There are other, smaller studies that could be done at the positional level or with respect to draft position; however, this is a good start, and shows us that the test results we’ll see in Indianapolis do have some level of relevance.

Welcome to 3SigmaAthlete.com — I’ll be talking about SPARQ, Approximate Value, the Combine, etc., and if you’re wondering what these things are, please refer to the FAQ section of the site. I’ve tried to lay out all methodology and relevant information there.

With Combine week upon us, there will be those who feel compelled to remind the masses that football is played in pads and not underwear, fought on a gridiron and not a track. To many people, the idea that such a complex sport could be influenced by a participant’s vertical jump or short shuttle time is laughable and quickly discarded. This isn’t entirely unreasonable, as there’s too much variability inherent in the career arc of any given prospect for there to be a universally accurate projection system.

This doesn’t mean that all athleticism data should be thrown out without examination. The best approach to the draft is to look at all available data, considering information with as little bias as possible. This should never be a scouting vs. analytics issue, but rather a scouting and analytics method.

Because listing things is much easier than writing points into the natural flow of an article, here’s a list of three keys ways in which analytics can inform the scouting process.

1. Players generally won’t succeed without a certain level of athletic ability, or “functional athleticism.”

One of the biggest stumbling blocks in draft season is the comparison to an outlier. They go something along the lines of:

“Anquan Boldin ran slow at the Combine and ended up being Anquan Boldin, so Young Slow Receiver X can also have a long and successful career!”

This isn’t necessarily a criticism of these comparisons. It’s difficult to avoid the outliers because, by their nature, outliers are the data points that stick in our minds. It’s easy to remember Anquan Boldin. The problem is that there aren’t many Anquan Boldins out there.

As discussed in the FAQ on this site, the z-score stat I cite is relative to the NFL positional average. This means that a z-score of 0 refers to a player who is athletically comparable to the 50^th-percentile NFL athlete. A 0 z-score is average, a -1 z-score is below average, and a -2 z-score is a real problem.

Drawing from a database of all players drafted since 1999 and using Approximate Value (explained in the FAQ) as a rough measure of ability, there has been 1 significant guard with a z-score below -1.5. There has been 1 significant center with a z-score under -1.5. There has been 1 significant offensive tackle with a z-score less than -1.5.

For running backs, you’re looking at Reuben Droughns and Domanick Williams as the most successful sub-1.5. At corner, Brent Grimes is just about the only successful player with a z-score that falls below -1.0.

Just listing names isn’t as powerful as actual data analysis, and I’ll get to that shortly. I’m simply trying to make the case that while the outliers exist, they’re much stronger in our memories than in reality. I don’t think every offensive lineman needs to test out like Lane Johnson, but the data shows that they need to at least meet a minimum athletic requirement.

2. More athletic athletes are better athletes.

Athleticism matters. It doesn’t matter in every case, for every Boldin or Wes Welker, but it generally matters. I’ve spent the last 10 months collecting and processing data in the hope of proving this correlation statistically, and I discuss the result in a piece at great length. While I find it all fascinating, you may not be as much into the t-tests and methodology. Here’s the plot and regression that I ultimately arrived at:

If you skipped the linked article, the x-axis (horizontal axis) represents athleticism and the y-axis (vertical axis) represents NFL production. What we see is that there’s a clear trend toward more athletic players producing a higher AV3. If there was no relationship between athleticism and production, this line would be flat, parallel to the x-axis (i.e., zero slope). This relationship is statistically significant with a p-value of approximately zero.

This doesn’t mean that the more athletic player is always going to produce at a greater rate. It means that consistently picking players from a more athletic group will yield more production over the long run.

Let’s look at the first page of the wiki page on analytics.

“Analytics is the discovery and communication of meaningful patterns in data.”

The goal is to find meaningful patterns in data, often on a large scale. We aren’t able to look at 5 players and make definitive rulings on their career paths at the Combine. Over the course of time, we want to make the best value propositions with our draft capital, and you will generally find more success consistently selecting from a pool of ‘plus’ athletes than average ones.

3. Analytics should make us ask questions and re-evaluate.

Analytical athleticism comparisons can help us look back at past evaluations and question what skill or ability makes the current prospect more able to adjust to the NFL.

We don’t have Combine values for Nelson Agholor yet, but, courtesy of data maven Tony Wiltshire, I have some rough numbers he put up at his USC junior day.

Now, we don’t know that Marqise Lee won’t be a good NFL player, and he struggled through injury in his rookie season. But we know that he’s a pretty similar athlete to Agholor, will probably slot in at a similar draft position, and didn’t have an overly impressive rookie season.

In this particular case, it’s not difficult to isolate the skill that differentiates Agholor from Lee: Nelson frequently catches the ball when it’s thrown to him. The athletic comp asks how the two players are different, and we’re able to answer the question.

There’s also the case of certain athletic profiles tending to produce a high number of successful NFL players. Jordan Matthews wasn’t generally regarded as an explosive athlete last spring, but his top 4 athletic comparisons showed that he probably had the requisite athleticism to be a good NFL player. Players built like Jordan Matthews tend to do pretty well.

This doesn’t mean that he’s necessarily going to be as good as AJ Green. The intent is to look back and question the initial evaluation. Is there something that shows up on the field that contradicts the results of his athletic testing? Is there a reason to grade down his future potential on an athletic basis?

For a given prospect, the athletic profile may not tell the full story, but it’s always worth looking at the numbers and going back to the initial evaluation.

Contrary to the beliefs held by some, analytics aren’t an attempt to replace scouting or based on a belief that everything is calculable with enough spreadsheet cells. The very best NFL evaluators consistently fail. It’s a difficult job, and the hit rate isn’t great for anyone. The use of analytics is an attempt to do things more efficiently, to get incrementally better at what we’re doing.

Combine week starts tomorrow, of course, so check back in later on and I’ll have a few previews and a recap of each testing day in Indy.